Hipercubo o teseracto

Si para los físicos la cuarta dimensión está representada por el tiempo, en el mundo de las matemáticas esas dos palabras tienen una connotación muy distinta. La geometría euclidiana prevé una o más dimensiones por encima de nuestro mundo en 3D en forma de teoría matemática. Esto es, aparte de las tres dimensiones conocidas (altura, anchura y profundidad), se supone como mínimo otra dimensión más, la cuarta en discordia, que cumpliría perfectamente las propiedades cartesianas, es decir, sería perpendicular a las otras tres y partiría de un origen de coordenadas común.

Nosotros no podemos siquiera imaginar cómo sería el mundo en 4D, porque estamos recluidos en un universo de sólo tres dimensiones. Si partimos de un sistema de coordenadas en el espacio 3D, tenemos un eje X que representa la anchura, un eje Y que es la altura y un eje Z que representa la profundidad. La cuarta dimensión vendría simbolizada por un hipotético eje W que, como decíamos antes, sería perpendicular a X, Y y Z. Algo que con nuestra mente es imposible comprenderlo porque pensamos y vemos en tres dimensiones. Pero ello no quiere decir que no exista una cuarta dimensión, sino simplemente que no podemos verla.

Imagina por un momento que no eres una persona, eres un cuadrado habitante de Planilandia, la genial novela de Edwin A. Abbott. Los cuadrados viven en el plano y sólo tienen dos dimensiones (ancho y largo), no conocen nada más. Un día, aparece volando por el espacio 3D (que tú no comprendes) un cubo y te saluda. Como él está por encima de ti y no concibes el concepto de altura, prácticamente creerás que te estás volviendo majareta.

Para hacerse visible, el cubo decide posarse sobre tu plano 2D. En ese momento tú verás surgir de repente un cuadrado a tu lado y te darás un susto inmenso, pues no sabes por dónde ni de dónde ha aparecido. Después de hablar unos minutos con él, le preguntas a ver por qué demonios se llama a sí mismo cubo, cuando lo que ves es un simple cuadrado como tú. Él te intentará explicar que lo que estás visualizando es una proyección de su figura 3D sobre tu mundo en dos dimensiones, e intentará proyectarse de manera inclinada, atravesando tu suelo, para ver si te haces una idea de su forma real. La imagen que tú verás en ese momento será la siguiente.

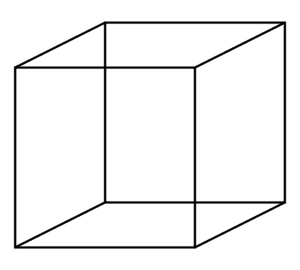
Cubo proyectado en un plano

No comprendes nada. Lo que antes era un cuadrado ahora se ha transformado en dos cuadrados que se cruzan y que tienen líneas inclinadas que unen sus vértices. No sabes mirar más allá del plano.

Vuelve al mundo real; eres una persona otra vez. De la misma forma que el cuadrado nunca podría imaginarse cómo es un cubo porque desconoce lo que es la tercera dimensión, nosotros no podemos comprender los elementos que componen la cuarta. Sabemos perfectamente que la proyección de un cubo sobre un plano genera una figura como la anterior, con unas líneas más largas y otras más cortas y ángulos diferentes. Sin embargo, podemos afirmar con total seguridad que en un cubo todas sus aristas son de igual longitud y todos sus ángulos son rectos (90º) porque vivimos en un mundo tridimensional y podemos palpar un cubo.

De la misma manera, geométricamente se puede demostrar la existencia de los llamados hipercubos (o teseractos) en cuatro dimensiones. Desde que vi, hace ya años, la segunda parte de la película Cube (Cube 2: Hypercube), los hipercubos se han metido en mi cabeza y ya no los puedo sacar de ahí. Es, probablemente, la figura más hermosa desde el punto de vista matemático y más quimérica desde el de la vida real. Por cierto, la primera de Cube es una de mis obras maestras cinematográficas de culto; no así tanto la segunda y la tercera.

La imagen que encabeza este post es la de un hipercubo. Bueno, técnicamente es la proyección de un hipercubo sobre nuestro espacio tridimensional. Aunque si queremos rizar más el rizo, como lo estás viendo en una imagen plana en la pantalla de tu ordenador, diríamos que es la proyección plana 2D de la proyección espacial 3D de un hipercubo en 4D. Vaya lío, madre mía.

Si cogemos un cuadrado y lo proyectamos en el espacio, dándole altura, conseguimos un cubo. Si proyectamos un cubo hacia el espacio de cuatro dimensiones conseguimos un hipercubo. El teseracto se considera un cubo desfasado en el tiempo, es decir, cada instante de tiempo por el cual se movió pero todos ellos juntos. Por supuesto no podemos ver un teseracto en la cuarta dimensión, porque vivimos solo en tres con la limitación mental de nuestros cerebros.

Al igual que le pasaba al cuadrado de Planilandia, vemos unas líneas más largas que otras y ángulos diversos en su proyección, sin embargo el hibercubo tiene todas sus aristas iguales y todos sus ángulos rectos. Además lo que hay entre el cubo interior y el cubo exterior son más cubos, todos ellos tan rectos y cúbicos como los tridimensionales. El teseracto tiene 16 vértices, 32 aristas, 24 caras y 8 células (éstas serían el equivalente a los cubos tridimensionales).

Lo que sí podemos hacer es desdoblar el teseracto tetradimensional para trasladarlo a nuestro espacio tridimensional. De la misma manera que somos capaces de cortar las aristas de un cubo y desdoblarlo en un plano bidimensional obteniendo una suerte de cruz latina formada por seis cuadrados, si hacemos lo mismo con un hipercubo el resultado es una cruz 3D de ocho cubos (células).

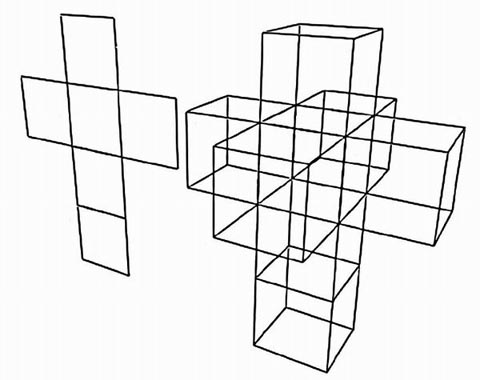
Cubo e hipercubo desdoblados

Lo que ya no podemos imaginar es ese engendro doblado sobre sí mismo, por la incapacidad ya comentada de comprender un espacio en cuatro dimensiones. Si tienes la mente muy abierta y necesitas un buen dolor de cabeza, la siguiente figura muestra el orden en el que deben coincidir las caras de los distintos cubos para conseguir el teseracto. Por supuesto, teniendo en cuenta que todas las aristas deben medir lo mismo y que todos los ángulos deben ser rectos. Algo imposible para nuestras cabezas de chorlito tridimensional.

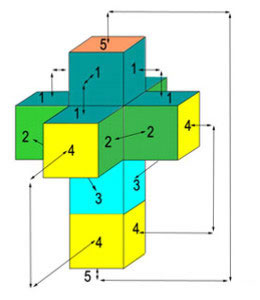
Orden para doblar un hipercubo

De la misma forma en que existen figuras geométricas en un supuesto mundo de cuatro dimensiones, ¿quién nos puede a nosotros asegurar que no existan otro tipo de manifestaciones «inteligentes» en él? Llámalo ente, alma, energía, mente o como quieras. Es posible que en un espacio tetradimensional haya entidades que sólo algunos de entre nosotros podemos ver bajo determinadas circunstancias y cuando se proyectan sobre nuestro espacio 3D. Es posible que los llamados fantasmas no sean más que seres 4D que están siempre ahí pero que no podemos ver más que cuando invaden nuestro espacio y que nos pegan terribles sustos como al pobre cuadrado cuando el cubo aparece de sopetón en su plano.

En fin, ese tema se lo dejamos a Iker Jiménez y a su parienta y nosotros nos quedamos con la versión matemática y geométrica del asunto que es mucho más factible.

Hasta el propio Dalí, que estaba un poco zumbado del bolo (sólo hay que ver sus cuadros), dibujó un hipercubo en una de sus obras, Corpus hipercubicus.

Corpus hipercubicus (Dalí)

Para terminar, os dejo un vídeo en el que el conocido astrónomo y divulgador científico Carl Sagan explica todo lo anterior de una forma más gráfica que un servidor. Vale la pena echarle un vistazo e invertir 7 minutos de nuestro tiempo para intentar comprender un poco mejor lo que la cuarta dimensión representa podría representar.

18 comentarios a “Teoría de la cuarta dimensión: el hipercubo”