Entradas de la categoría ‘Ciencia’
Generando electricidad hace 2.200 años

Antigua batería de Bagdad
El envoltorio cuproso estaba sujeto al cuello de la vasija por algo parecido al betún, sobresaliendo un centímetro, y daba la impresión de haber estado revestido con una fina película de plomo. Los arqueólogos no supieron dar explicación a aquel descubrimiento, así que enviaron una muestra al Museo Nacional de Iraq para que lo investigaran más a fondo. Tres años más tarde, en 1939, y tras multitud de pruebas y reproducciones, el director del museo (a la sazón el alemán Wilhelm König) lanzó la noticia bomba que conmocionó a todos los científicos del mundo: aquello podría tratarse de la primera y más antigua batería de la historia. Desde entonces, aquel descubrimiento pasó a conocerse como la batería de Bagdad, a veces denominada batería parta también.
Se especuló con que el comportamiento del instrumento era exactamente igual que el de una pila eléctrica actual, pudiéndose haber unido varios de ellos en serie para aumentar el voltaje producido; no en vano, König relacionó el descubrimiento con multitud de varillas de cobre y cilindros de hierro similares procedentes de Mesopotamia. La corrosión que presentaban los cilindros metálicos del interior se supuso producida por algún tipo de elemento cítrico contenido en las vasijas, lo que actuaría como electrolito para generar electricidad.
El cobre y el hierro forman una muy buena pareja electroquímica, de modo que, en presencia de cualquier electrolito o solución iónica, son capaces de generar potencial eléctrico. De ello se encarga la llamada corrosión galvánica, un proceso en el que un metal menos noble, en presencia de otro más noble y de un electrolito, se corroe. Esta corrosión (que no es más que un movimiento de iones desde el ánodo hasta el cátodo) se aprovecha en pilas y baterías para generar una corriente de cierto voltaje.

Esquema y reproducción de las baterías
Willard Gray, ingeniero estadounidense de la época, decidió tratar de hacer una réplica de las baterías después de apoderarse de algunos dibujos y planos del dispositivo realizados por el científico alemán Willy Ley. Rellenó el recipiente con sulfato de cobre y consiguió generar medio voltio de electricidad. Posteriormente declaró que, en los tiempos en los que se fabricaron las baterías originales, se podría haber utilizado otro líquido cítrico a modo de electrolito al alcance de los habitantes del momento, como, por ejemplo, zumo de uva corriente. Treinta años más tarde, el científico alemán Arne Eggebrecht volvió a reproducir el dispositivo, consiguiendo 0,9 voltios, con vinagre como electrolito.
Sin embargo, desde aquel momento hubo una corriente escéptica en favor de otras explicaciones más lógicas para aquellos instrumentos. Nunca se descubrió, en ninguna excavación, material alguno que hubiera podido funcionar como unión entre varias baterías (como cables metálicos), por lo que la conexión en serie quedó descartada. Además, ¿para que demonios iban a necesitar electricidad hace dos mil años?
La explicación más lógica a las baterías de Bagdad la ofreció el propio Willard Gray cuando afirmó que, en su reproducción de las vasijas, había introducido una estatuilla de plata en el interior que, dos horas después, se había vuelto de color dorado o cobrizo. Según él, había demostrado que la batería funcionaba y que su probable uso era el destinado a restaurar objetos de plata, lo que hoy conocemos como galvanización o galvanizado.
Sin embargo, y para vapuleo de esta información, científicos posteriores a Gray demostraron que, con el electrolito utilizado y la corriente generada, era imposible que en dos horas se pudiera haber galvanizado nada. Además, recordaron que en ningún lugar de estudio arqueológico en el mundo se ha encontrado jamás objeto alguno galvanizado.
Los más radicales afirman que esas vasijas se utilizaban simplemente para guardar legajos o cosméticos. El betún que tapa la boca de las vasijas, dicen, es aislante eléctrico, por lo que sería imposible sacar la electricidad hacia fuera sin modificar el diseño. Además, una celda galvánica requiere de un rellenado más o menos continuo de electrolito, por lo que habría sido una solemne tontería haber sellado herméticamente las vasijas con dicho betún. Es posible, afirman, que pergaminos guardados en estos recipientes se pudrieran por completo en su interior, dejando probablemente un rastro de residuos orgánicos ligeramente ácido.
Durante la invasión de Iraq del año 2003, llevada a cabo por una coalición de países encabezada por EE. UU., y que marcó el inicio de la Guerra de Iraq, el Museo Nacional fue asaltado y saqueado, perdiéndose infinidad de piezas de un valor incalculable, entre ellas las baterías de Bagdad. No se sabe a ciencia cierta qué es lo que fue de ellas y, aunque algunas versiones afirman que pudieron ser retiradas para su protección por el mismo gobierno iraquí como medida de protección ante los bombarderos, los más escépticos consideran que pasaron a formar parte del tráfico ilegal de antigüedades mesopotámicas. Una auténtica pena.
La termodinámica de un botijo

Con ustedes, el botijo
Consiste en un recipiente de arcilla o barro poroso, de formas redondeadas y base comúnmente circular, que posee un asa de agarre y dos aberturas, una más ancha para echar el agua (boca) y otra más estrecha para beber (pitorro o pitón), inclinándolo por encima de la boca.
La procedencia etimológica de su nombre es romana, concretamente del término del latín tardío buttis (odre). De este mismo derivan también «bota» (la de beber), «botija» y, finalmente, «botella».
El botijo tiene la particular cualidad de enfriar físicamente el agua que contiene aun en los climas más cálidos, ya que puede llegar a reducir su temperatura interior hasta 10 grados en condiciones óptimas. Pero, ¿cómo demonios funciona un botijo? ¿Es posible que algo tan antiguo siga las leyes de la termodinámica? Pues sí, mire usted.
El mecanismo de enfriamiento es tan sencillo como compleja es su formulación matemática. El agua contenida en un botijo, al ser éste de un material poroso, se filtra hacia la superficie exterior donde, por efecto de las altas temperaturas, se evapora. Este cambio de estado líquido a gaseoso necesita de energía calorífica, y parte de esta energía se extrae de la propia masa de agua contenida en el interior, disminuyendo su temperatura. Ni más ni menos.
La teoría cinética nos permite interpretar también el fenómeno de refrigeración por evaporación desde el punto de vista microscópico o molecular. Así, nos encontramos con que las partículas de un sólido, líquido o gas se están moviendo o agitando continuamente. La temperatura es una medida de la energía cinética media de las partículas:mayor velocidad de éstas implica mayor temperatura, y viceversa. En un líquido las partículas se mueven deslizándose unas sobre otras, las más veloces se acercan a la superficie libre del líquido y, si tienen energía suficiente, pueden escapar de él, produciéndose la evaporación. Este cambio de estado (de líquido a vapor) provoca un enfriamiento del sistema, ya que, precisamente, desaparecen las partículas más energéticas.
El grado de enfriamiento depende de varios factores, fundamentalmente del agua que contenga el botijo y de las condiciones ambientales. Estas últimas deben implicar un clima cálido pero seco, es por ello que en la zona norte de España no tuviera tanta repecursión la utilización del botijo, porque la humedad ambiental dificulta la evaporación y, por lo tanto, la refrigeración del líquido elemento. El botijo, pues, es un elemento típico de la cultura española sobre todo en el tercio sur de la península (Extremadura, La Mancha, Levante y Andalucía). Sin embargo, difícilmente nos encontraremos una región o comarca que no tenga su botijo.
Asimismo, como hemos comentado, el material utilizado para la fabricación del botijo ha de ser poroso, por aquello de que el agua pueda filtrarse desde el interior hacia el exterior. Por tanto, los botijos esmaltados, lacados o pintados que hoy se utilizan como motivos ornamentales pierden sus capacidades refrescantes en cuanto son decorados.
Por el mismo efecto físico, las cantimploras metálicas de montañeros y exploradores enfrían el agua que llevan dentro. En este caso, el material en el que están fabricadas no es poroso, por lo que se les añade un abrigo o forro de fieltro que ha de ser humedecido convenientemente. El agua con el que se moja la tela se evapora de la misma manera que la de un botijo tradicional, utilizando parte de la energía calorífica del líquido que contiene la cantimplora para convertirse en vapor, refrigerando así el contenido.
En realidad es un fenómeno que existe desde que el mundo es mundo, y que está más cerca de nosotros de lo que pensamos. Nuestro propio mecanismo de refrigeración natural funciona de la misma manera, pues miles de gotitas de sudor (generadas por nuestras glándulas sudoríparas ecrinas de todo el cuerpo y enviadas hacia los poros de la piel) nos perlan de agua que, en el proceso de vaporización cuando la temperatura exterior es alta, utilizan nuestro propio calor como energía para evaporarse, rebajando nuestros grados corporales. ¿Qué cosas, eh?
Pero lo más curioso del tema es que, en el año 1990, un profesor de Química en la Escuela Técnica Industrial de la Universidad Politécnica de Madrid, el señor Gabriel Pinto, se empeñó en parametrizar en una ecuación matemática todas las variables y factores que influyen en el mecanismo refrigerador del botijo. Pinto desarrolló un modelo matemático que iba ajustando mediante datos experimentales. Había considerado multitud de factores, empero, existía algo que seguía sin cuadrar: las ecuaciones le conferían al botijo una capacidad ilimitada de enfriar.
Fue entonces cuando otro profesor de Química, José Ignacio Zubizarreta, aportó el detalle que faltaba, algo que Pinto había pasado por alto: el calor de radiación que aporta el aire que se encuentra en el interior del recipiente. La fórmula estaba terminada. En 1995, ambos profesores publicaron en la revista americana Chemical Engineering Education (en su número 29) el artículo titulado An ancient method for cooling water explained by means of mass and heat transfer. El resultado fue un par de ecuaciones diferenciales que relacionaban todos los parámetros; las que se pueden observar en la imagen siguiente.
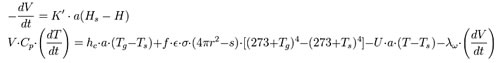
Las ecuaciones del botijo; ahí es nada
Donde:

Suponiendo un botijo con geometría esférica perfecta, el siguiente esquema puede ayudar a comprender las ecuaciones.
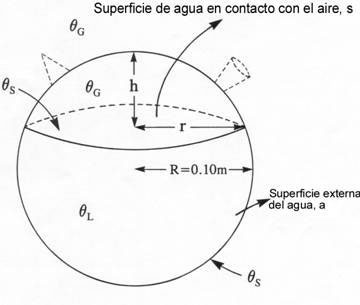
Gráfico botijero
De ahora en adelante, siempre habremos de mirar a los botijos con otros ojos. Y con esto termino, y aludo a otra entrada de este blog que remata la afirmación aquella de que la física de los instrumentos modernos, la química de los seres vivos o la mecánica de los aparatos actuales siempre estuvieron ahí, esperando a que alguien los repitiera artificialmente y los plasmará en un papel. Nada nuevo bajo el sol.
El aerógrafo prehistórico (o el efecto Venturi en el Paleolítico Superior)

Manos en negativo (Altamira)
Resulta curioso, cuando menos, comprobar cómo los descubrimientos científicos documentados y verificados tienen mucho de documentados, mucho de verificados pero poco de descubrimientos. La física de los instrumentos modernos, la química de los seres vivos o la mecánica de los aparatos actuales siempre estuvieron ahí, esperando a que alguien los repitiera artificialmente y los plasmará en un papel, asignando su nombre al hallazgo para la posteridad. Pero ello no quiere decir que antes no hubiera habido otro que, por casualidad, descubriera lo mismo y lo utilizara profusamente, sin haber estampado su firma en un legajo junto a su fortuito encuentro; muchas veces porque ni siquiera, en ese momento, se había inventado el papel.
Es el caso, entre otros muchos, del aerógrafo prehistórico. Si uno se da una vuelta por la cueva de Ardales (Málaga), por la de Maltravieso (Cáceres), por la cueva de Altamira (Cantabria) o por la de Tito Bustillo (Asturias), podrá comprobar como en las propias cavidades horadadas en la roca (si es que son visitables) o en los museos cercanos, se le muestra uno de los descubrimientos arqueológicos más curiosos y que más trajo de cabeza a los expertos durante años: las pinturas de manos en negativo.

Mano en negativo (Pech Merle, Francia)
Estos dibujos, como se puede comprobar en la imagen anterior, son representaciones de manos de los antiguos habitantes paleolíticos de las cuevas. Sin embargo, y como cabría esperar, la pintura no ha sido plasmada cubriendo la palma de tinte y estampándola contra la pared, puesto que lo pintado aparece alrededor de la figura de la mano, dejando el hueco ocupado por ésta sin teñir. De ahí su denominación de «manos en negativo».
El descubrimiento hizo pensar mucho a los arqueólogos de hace décadas. Lo primero que se investigó fue el pintado periférico, es decir, se supuso que el autor habría colocado la mano en la roca y, con un dedo de la otra mano impregnado en una tintura, habría ido coloreando la periferia. La hipótesis se desechó enseguida, porque las pruebas que se llevaron a cabo no producían manos como aquellas. Las originales parecían haber sido creadas no a base de pinceladas, sino por la expulsión violenta de pintura sobre la mano, dejando esa mancha característica alrededor.
La segunda hipótesis hizo a los expertos realizar la prueba por medio del soplado de tinte sobre la mano en la pared, lo que se conoce como técnica del estarcido. Una delgada pajita, que podría ser un pequeño hueso perforado, hacía las veces de conducto por el que escupir la pintura a presión desde la boca del artista. Sin embargo, aquella prueba tampoco resulto nada concluyente. La mancha de colorante se formaba por gotas de variado tamaño, inconexas entre sí y de aspecto tosco y burdo. No era una imagen tan homogénea como la de las manos de los hombres prehistóricos, representadas por diminutas partículas de pintura como si se hubiera producido una pulverización con nuestros aerosoles actuales. ¿Cómo es posible que aquella gente utilizara alguna técnica que hoy en día no somos capaces de reproducir?, se preguntaban los arqueólogos.
Una tercera vertiente defendía un procedimiento que emplearía un pincel o brocha, fabricado con pelo de caballo, agitado enérgicamente, salpicando la pared y dejando el hueco de la mano limpio. Los resultados tampoco fueron los esperados.
Al fin, y gracias a varios hallazgos cercanos a las pinturas en los que aparecían los instrumentos utilizados (un cuenco y dos pequeños huesecillos de ave huecos), la incógnita pudo ser despejada. Los hombres paleolíticos habían descubierto el denominado efecto Venturi algunas decenas de miles de años antes de que el reconocido físico italiano le pusiera su nombre.
Como diría nuestra amiga la Wikipedia, el efecto Venturi se explica por el principio de Bernoulli y el principio de continuidad de masa. Si el caudal de un fluido es constante pero la sección disminuye, necesariamente la velocidad aumenta tras atravesar esta sección. Por el teorema de la conservación de la energía mecánica, si la energía cinética aumenta, la energía determinada por el valor de la presión disminuye forzosamente.
Este efecto es fácilmente reproducible con instrumentos básicos: un par de pajitas pequeñas y un cuenco con algún pigmento desleído en agua. Uno de los tubitos ha de tener un extremo sumergido en el líquido, el otro se coloca perpendicular al anterior y junto a él, quedando los centros de los orificios, pues, perpendiculares y separados por un milímetro o menos. Se sopla enérgicamente y se produce la pulverización. Es exactamente la misma técnica de la que se sirven los aerógrafos actuales.
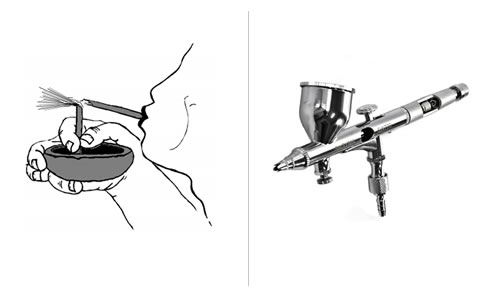
El antes y el ahora de la aerografía
Físicamente, al soplar con fuerza por el tubo horizontal, la velocidad del aire hace que la presión disminuya en el extremo superior del tubo vertical. La diferencia de presiones resultante en ambos extremos de este tubo produce que la columna de tinte ascienda, empujada por la presión atmosférica. Cuando la pintura sube, se encuentra con el chorro de aire y se produce la salida pulverizada de la misma.
Las primeras manos en negativo conocidas se representaron en las cuevas de Cosquer (Marsella) y Gargas (Pirineos de Ariége) hace aproximadamente 27.000 años. Los principales conjuntos de este tipo de pintura prehistórica en la Península Ibérica se realizaron en fechas posteriores, coincidiendo con el Magdaleniense. Si bien es cierto que el foco más importante de manos en negativo se desarrolló en la región franco-cantábrica, existen importantes ejemplos en la Patagonia, Italia, Austria, Borneo, Norte de África, Urales o la India.
Aquellos antiguos habitantes de nuestro mundo nunca supieron lo importante que el efecto Venturi llegaría a ser para nuestras vidas actuales (carburadores de automóviles, pistolas de pintura, duchas de alta eficiencia, dispositivos antifugas para lavadoras, etcétera), pero tampoco supieron discernir la física del invento. Simplemente soplaban y utilizaban una tecnología que, probablemente, descubrieran por casualidad [modo 'Iker Jiménez' ON] les fuera entregada por seres inteligentes provenientes de otras dimensiones [modo 'Iker Jiménez' OFF].
Os dejo con un vídeo demostrativo en el que unas jovenzuelas colegiales explican perfectamente, y de una forma práctica, todo lo anteriormente comentado. Eso sí, con mucho guión y muy poquita naturalidad escénica, la verdad. Pero sirve.
Demostración del aerógrafo prehistórico
Dalí y sus obsesiones matemáticas

Salvador Dalí
Salvador Dalí no era un pintor al uso, ni siquiera para la época y estilo que le tocó vivir. Enamorado de la ciencia, atesoraba en su biblioteca decenas de libros que trataban de geometría, matemática o biología. Asistió en su vida a multitud de descubrimientos científicos como el del ADN, la teoría cuántica, los modelos atómicos o el concepto de antimateria, y todos ellos causaron un profundo impacto en él, dejando una huella más o menos visible en su obra.
Una de las mayores obsesiones para Dalí a la hora de generar sus cuadros fue la de la razón áurea. Esta proporción, de historia milenaria, define la relación existente entre dos divisiones de un segmento y la representa por medio del número φ (letra griega fi), un valor algebraico irracional que, aproximadamente, es 1,618033.
Desde la Gran Pirámide de Guiza, en Egipto, hasta las estructuras formales en la ‘Quinta Sinfonía‘ de Beethoven, pasando por el Partenón de Atenas, la ubicación de las «efes» en la construcción de violines, el ‘Hombre de Vitruvio‘ de Leonardo da Vinci o las relaciones entre altura y anchura en las obras de Miguel Ángel. Todos ellos, y muchos más, son ejemplos en los que los expertos han visto indicios o evidencias de la utilización de la divina proporción o proporción áurea.
Dalí plasmó esta inquietud en cuadros como ‘Semitaza gigante volante, con anexo inexplicable de cinco metros de longitud’ (óleo sobre lienzo, 1944-1945), una pintura en la que los motivos más destacados van apareciendo inscritos en la sucesión decreciente de rectángulos áureos que resultan al extraer, sucesivamente, un cuadrado al rectángulo anterior.
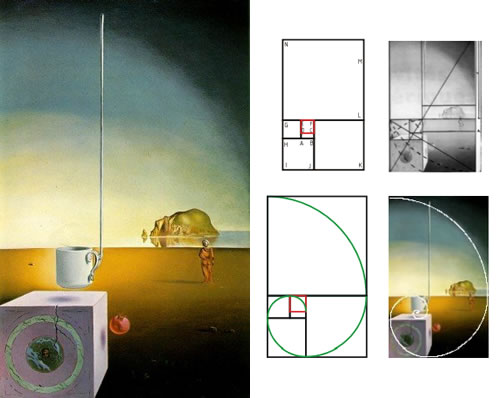
'Semitaza gigante volante, con anexo inexplicable de cinco metros de longitud'
Esta obra se puede considerar como un homenaje, no carente de humor, al rectángulo de oro. No sólo se puede descomponer el cuadro en una serie de rectángulos áureos sino que, además, los diferentes elementos del dibujo son la llave que permite reconstruir estos rectángulos. A partir del diseño de la taza se obtiene una sucesión de rectángulos áureos que nos conduce a una espiral áurea, la cual termina en la sombra negra de la parte alta de la pintura.
Por otro lado, ese «anexo inexplicable» del título del cuadro y que sale del asa de la taza, obligando a prolongar el dibujo hacia arriba, es, en realidad, totalmente explicable: las dimensiones del cuadro (50 × 31 centímetros) están en proporción áurea, siendo tal anexo el elemento que justifica dichas dimensiones.
La pintura titulada ‘Leda atómica’ (óleo sobre lienzo, 1949) es otro buen ejemplo de lo anteriormente explicado. Dalí realizó este cuadro con ayuda del matemático rumano Matila Ghyka, que le ayudó a sobrellevar tres meses de complicados cálculos teóricos que dieron lugar a la peculiar composición del óleo. La pintura sintetiza siglos de tradición matemática y simbólica, especialmente pitagórica. Se trata de una filigrana basada en la proporción áurea, pero elaborada de tal forma que el espectador no la aprecia a simple vista. En el boceto de 1947 (lápiz y tinta sobre papel) se advierte la precisión del análisis geométrico realizado por Dalí basado en el pentagrama místico pitagórico, el cual es una estrella de cinco puntas dibujada con cinco trazos rectos.

'Leda atómica'
Asimismo, el pintor realizó varias obras en las que incluía el cuerno de rinoceronte como elemento recurrente, cuerno que Dalí consideraba como una curva logarítmicamente perfecta. Ejemplos de ello son ‘La encajera de Vermeer’ (óleo sobre lienzo, sobre madera, 1955), ‘Cuernos azules. Diseño para un pañuelo’ (Aguada, 1955) o ‘Figura rinoceróntica de Ilisos de Fidias’ (óleo sobre lienzo, 1954).
Relacionada con la proporción áurea, otra de las obstinaciones pictóricas de Dalí fue la de la figura geométrica del dodecaedro, un poliedro convexo de doce caras que son pentágonos regulares, esto es, de lados iguales y ángulos internos congruentes. Su obra maestra relacionada es ‘La última cena’ (óleo sobre lienzo, 1955). En este cuadro, Dalí utilizó la proporción áurea en la razón de sus dimensiones y en las dimensiones que forma la línea recta de la mesa. Además, el dodecaedro se convierte en el escenario que envuelve la escena; doce caras como doce eran los apóstoles.
Según Platón, el dodecaedro representa la quintaesencia, puesto que en él se pueden inscribir el resto de los poliedros regulares: cubo, tetraedro, octaedro e icosaedro, que simbolizan los cuatro elementos del universo: tierra, fuego, agua y aire. Así mismo, si se unen los centros de las caras de un dodecaedro entre sí, se forman tres rectángulos cuyas proporciones son las del número áureo.

'La última cena'
Igualmente, la materia de las dimensiones obsesionó no sólo a Salvador Dalí en su obra, sino también el resto de pintores de su época y de épocas anteriores. El hecho de poder plasmar una correcta perspectiva en tres dimensiones sobre un lienzo bidimensional, consiguiendo una imagen realista del motivo plasmado, hacía recurrir a los artistas a tratados geométricos con asiduidad. Cézanne, Seurat y, de hecho, casi todos los pintores que a finales del siglo XIX y principios del XX trabajaban estos temas, sólo estaban interesados en el problema desde el punto de vista de la representación pictórica. Dalí quería ir más allá.
El pintor catalán se obsesionó con una cuarta dimensión geométrica, que terminó por plasmar en su obra ‘Crucifixión’, también conocida como ‘Corpus hypercubus’ (óleo sobre lienzo, 1954). Un hipercubo, o teseracto (del que se habló largo y tendido ya en este blog), es una figura geométrica en una hipotética cuarta dimensión cartesiana que no podemos imaginar, pues la teoría matemática que la arropa es demasiado compleja para los seres humanos que vivimos en sólo tres dimensiones.

'Corpus hypercubus'
El hipercubo tiene 16 vértices, 32 aristas, 24 caras y 8 células. Estas últimas ocho células se corresponden con ocho cubos tridimensionales, que son los que forman la cruz de la crucifixión de Jesucristo en el cuadro. En realidad, lo que vemos ahí es un teseracto de la cuarta dimensión desdoblado en el espacio tridimensional (así como un cubo 3D desdoblado forma una cruz latina de seis cuadrados). Para formar el hipercubo habría que unir las caras de la figura, retorciéndola, consiguiendo algo muy difícil de concebir en nuestra mente, por no decir imposible.
En el óleo, el hipercubo desdoblado resulta ser la cruz de la muerte, y su sombra en el suelo forma una cuadrícula bidimensional en forma de cruz latina, lo que denota la fijación que tenía el pintor por la transición entre dimensiones.
Como se puede observar, al igual que todos los grandes genios del arte, Salvador Dalí ocultó mensajes en sus obras, en este caso de carácter matemático. Y es que, además de lo expuesto, el pintor jugó también con la geometría fractal, como en su cuadro ‘El rostro de la guerra’ (óleo sobre lienzo, 1940); la geometría proyectiva, en ‘Las llamas llaman’ (óleo sobre lienzo, 1942); la topología, en ‘Contorsión topológica de una figura femenina’ (óleo sobre lienzo, 1983); o la Teoría de las catástrofes, de René Thom, como en ‘La cola de la golondrina’ (óleo sobre lienzo, 1983).
Dalí falleció el 23 de enero de 1989, dejando tras de sí una complicada y prolífica obra en la que fusionaba arte y ciencia. Sin duda un loco muy cuerdo.
Esta entrada no tiene título

Botones paradójicos
A Epiménides se le atribuye una frase que da pie a una contradicción lógica: «Todos los cretenses son unos mentirosos». Si se admite que los mentirosos mienten siempre, mientras que las personas que dicen la verdad también lo hacen siempre, la afirmación del poeta responde a la primera paradoja del mentiroso (también conocida como Paradoja de Epiménides) de la que se tiene constancia.
Con semejante hipótesis, la declaración de Epiménides no puede ser verdadera, pues él era cretense y, por consiguiente, al afirmar tal cosa estaría mintiendo, siendo falsa su afirmación. Sin embargo, tampoco puede ser falsa, porque se deduciría entonces que todos los cretenses dicen siempre la verdad, y, por consiguiente, lo que dice el cretense sería verdad, que todos son unos mentirosos. La pescadilla que se muerde la cola.
Los griegos se daban de cabezazos contra la pared cuando escuchaban algo así, y es que gustaban tanto de una lógica perfecta, en la que toda proposición fuera verdadera o falsa, sin más, que los enunciados de apariencia perfectamente clara que eran tan contradictorios les hacían enloquecer. Otro poeta y filólogo alejandrino, Filetas de Cos (siglos III y IV a. de C.), se fue de manera temprana a la tumba a causa de la angustia que este tipo de paradojas le causaban. Dice que su epitafio rezaba «Soy Filetas de Cos. Me hicieron morir el Mentiroso y las noches de insomnio por su causa».
Otros autores atribuyen la primera manifestación de la paradoja del mentiroso a Eubulides de Mileto (siglo IV a. de C.), filósofo griego de la escuela megárica, cuando aseveró «Si afirmo que estoy mintiendo, ¿miento o digo la verdad?». Además, estos autores aseguran que la aseveración de Epiménides no responde al cien por cien a la paradoja del mentiroso. El error de la formulación de la Paradoja de Epiménides es suponer que la falsedad de «todos los cretenses mienten» implica la verdad de «todos los cretenses dicen la verdad», cuando esto no es así. El enunciado «todos los leones viven en África» es falso en el momento en el que haya un sólo león viviendo fuera de África, es decir, no es necesario que todos los leones vivan fuera de África para que la afirmación «todos los leones viven en África» sea falsa. Lo mismo ocurre con «todos los cretenses mienten», y debemos tenerlo en cuenta a la hora de formular esta paradoja. De la primera manera, la paradoja es correcta, aunque algo compleja; de la segunda manera es sólo una apariencia de paradoja.
Lo cierto es que la paradoja del mentiroso ha llegado hasta nuestros días en forma de múltiples enunciados que pasamos por alto. Existen pegatinas para parachoques de automóviles que rezan «¡Ya está bien de pegatinas en los parachoques!», anuncios en prensa con el texto «No lea este anuncio» a modo de reclamo, normas de buen estilo literario que dicen «No use comas, que no sean necesarias» o títulos de entradas de blog que manifiestan «Esta entrada no tiene título». Llegaron a hacerse bastante populares, en los años noventa, aquellas chapas con imperdible para colgar en la ropa que decían «Chapas no»; así como las pintadas en paredes que clamaban «¡Basta ya de pintadas!». Y otros ejemplos que se pueden encontrar magistralmente recogidos en el libro ‘¡Ajá! Paradojas que hacen pensar‘, de Martin Gardner (RBA, 2009).
Un despacho de la agencia internacional de noticias UPI, en 1970, daba cuenta de que en unas elecciones de Oregón se permitía a los candidatos imprimir en las papeletas de voto un lema de hasta 12 palabras debajo de su nombre. He aquí el de Frank Hatch, candidato al Congreso por los demócratas: «No deberían figurar aquí quienes pierden tiempo ideando lemas de doce palabras». Con sus doce palabras exactas.
Está claro que desde hace siglos hasta nuestros días, paradojas como esta nos acompañan y, también, nos acompañarán en el futuro. Muchas veces pasan desapercibidas, pero están ahí, y si se nos ocurriera dar vueltas a cada oración impresa que nos encontremos, probablemente nos volveríamos tan locos como los griegos. O no. Paradojas de la vida.

