Pi

Para los estudiantes del bachillerato actual diremos que π señala las veces en que el diámetro de un círculo cabe en su circunferencia. Ahora sí, ¿verdad? Hacemos un redondel con una cuerda y la estiramos en el suelo. Luego marcamos los diámetros sobre la cuerda y comprobamos que nos caben 3 y un poquito más. Eso es π. El siguiente GIF animado es totalmente esclarecedor.

Explicación gráfica de Pi muy sencilla de entender

En fin, nos unimos al carro de aproximaciones de π, pero no para intentar descubrir el decimal seiscientos trillones, sino para conocer el algoritmo Chudnovsky, uno de los más modernos métodos de calcular decimales de π. Algoritmos para este menester ha habido infinidad de ellos desde que el mundo es mundo, empezando por el de Arquímedes y pasando por los de Euler, Newton o Gauss (sí, el de las campanas).

El algoritmo Chudnovsky, descubierto por los hermanos David y Gregory Chudnovsky, matemáticos ucranianos, parece ser el más empleado en los cálculos de alta precisión de dígitos de π a comienzos de este siglo XXI en el que nos encontramos. Se fundamenta en una fórmula del hindú Ramanujan e implementa una serie de convergencia rápida siguiendo una serie hipergeométrica. Su fórmula es la siguiente:

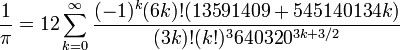
Algoritmo matemático Chudnovsky

Como se puede comprobar, no es más que un sumatorio sobre k desde 0 hasta infinito (∞), donde se hacen una barbaridad de operaciones en función de k en cada iteración. Cada término de esta fórmula añade 14 decimales exactos al valor calculado de π; k es una proporción entre la precisión en decimales que necesitemos calcular y el valor límite de 14. Es una fórmula incluida en el famoso software Mathematica, de uso común en el ámbito científico.

Lo que se detalla a continuación es un pequeño código en Visual Basic que nos permite extraer el valor exacto de π con sus catorce primeros decimales haciendo uso de la fórmula de los hermanos Chudnovsky. Es muy sencillo de entender, ya que sólo sigue paso a paso el algoritmo. Destacar únicamente la función auxiliar Factorial para calcular los factoriales requeridos.

Código Visual Basic

Private Sub Chudnovsky()
    Dim k As Long
    Dim numeroPI As Double
    Dim Numerador As Double, Denominador As Double
    Dim Precision As Double, Limite As Double

    k = 0: numeroPI = 0
    Precision = 14
    Limite = (Precision + 3) / 14

    Do While k < Limite
        Numerador = 0
        Denominador = 0

        Numerador = ((-1) ^ k) * Factorial(6 * k) * (13591409 + (545140134 * k))
        Denominador = Factorial(3 * k) * (Factorial(k) ^ 3) * (640320 ^ ((3 * k) + (3 / 2)))

        numeroPI = numeroPI + (Numerador / Denominador)

        k = k + 1
    Loop

    numeroPI = 12 * numeroPI
    numeroPI = 1 / numeroPI

    Debug.Print FormatNumber(numeroPI, 14)
End Sub

Private Function Factorial(numFactorial As Long) As Double
    Dim i As Long, TempFactorial As Double
    TempFactorial = 1

    For i = 1 To numFactorial
        TempFactorial = TempFactorial * i
    Next i

    Factorial = TempFactorial
End Function

Que nadie intente calcular más de catorce decimales porque precisamente ese es el límite de las variables de doble precisión en Visual Basic. Eso sí, se puede extraer un número inferior alterando el valor de la variable Precision.

Los hermanos Chudnovsky, actualmente, residen en Estados Unidos y, además de por su habilidad en la construcción de supercomputadores caseros, son conocidos por la estrecha relación laboral que ambos mantienen, llegando a definirse ellos mismos como «un único matemático ocupando dos cuerpos». Esta colaboración también está marcada, en cierta medida, por la enfermedad de tipo muscular que sufre Gregory, que lo hace en ocasiones dependiente de su hermano David. De este último se ha llegado a decir que es el mejor matemático vivo de la historia.

Los cerebritos calculines continuarán su gesta de intentar llegar al final del número π, hasta el último decimal que lo convierta en un número irracional transcendente de valor concreto. O quizás tengan razón aquellos que aseguran que los decimales de π no se acabarán nunca, y que dicen que es un número tan complejamente apasionante que, por ejemplo, todos los números de teléfono del mundo se pueden encontrar escondidos en la secuencia decimal de π, porque sus dígitos parecen estar repartidos aleatoriamente y no construidos de una forma particular (encontrándose entre sus infinitos guarismos cualquier secuencia posible). O es probable que todos ellos tengan razón y ninguno de ellos la tenga, aunque seguramente la longitud de π acabará siendo bastante mayor que el título de este post (aunque parezca mentira).

Lo que está claro es que π es, para muchos, un número mágico donde buscar mensajes ocultos, y para todo el mundo un valor importantísimo que permite construir carreteras y barcos, entre otras muchas cosas. Su número de decimales importa poco a niveles prácticos hoy en día, porque sería una locura realizar cálculos con tal nivel de exactitud, además de una estupidez supina. Pero, por lo menos, vamos observando nuestra amplia evolución desde hace un par de miles de años, cuando se deducía de la mismísima Biblia que el valor de π era simplemente igual a 3; en Primera de Reyes, 7-23, dice literalmente:

Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos.

Por último, y ya que estamos en ello, recomendar desde aquí la película «Pi, fe en el caos«, una obra de arte geek y profundamente paranoica y demente, pero que todo buen friqui tecnológico debe visionar. Especial atención a sus múltiples fallos, comenzando desde el principio por el más garrafal de todos.

EDITANDO ANDO (17/09/2010): Se acaba de superar del récord de decimales de π calculados mencionado en esta entrada. Además ha sido a lo bestia, porque de 5 billones hemos pasado a 2.000 billones; casi na. El mérito es para un currela de Yahoo que se ha aprovechado de la infraestructura tecnológica de su empresa para tal menester. Así cualquiera.

9 comentarios a “Utilizando el algoritmo Chudnovsky y Visual Basic para calcular los catorce primeros dígitos decimales de Pi sin despeinarse (y otros chismes y cotilleos varios)”