-0

Es curioso que en nuestro mundo cuadriculado de aritmética ordinaria, el cero (0) es cero y punto pelota. No tiene sentido un valor de nada con un signo, porque nada es eso, absolutamente nada. Sin embargo, en el mundo del desarrollo informático, y también de algunas ciencias experimentales (y de determinadas aplicaciones teóricas en la física estadística y otras disciplinas), algunas representaciones numéricas permiten la existencia de un cero negativo (-0), distinguiéndolo a la perfección del cero positivo (+0) y considerándolos dos valores diferentes. El concepto de cero con signo es contrario a la suposición general de la mayoría de los campos de matemáticas de que el cero negativo es lo mismo que cero.

El estándar de la IEEE para aritmética en coma flotante (IEEE 754) es el más extendido para las operaciones en doble precisión o punto flotante (un método de representación de números reales). Este estándar define formatos para la representación de números en coma flotante (incluyendo el cero) y valores no normalizados, así como valores especiales como infinito y NaN (Not a Number), con un conjunto de operaciones que trabaja sobre dichos valores.

El IEEE 754, presente en la mayoría de los ordenadores y de los lenguajes de programación, define pues un -0 y un +0. Estos dos ceros pueden ser considerados como una variante del conjunto extendido R de los números reales, que añadía dos elementos nuevos al conjunto básico R de números reales, el +∞ y el −∞. El menos cero se basa en el concepto de análisis matemático de acercarse a 0 desde abajo como un límite y, asimismo, puede ser utilizado, de manera informal, para referirse a un número negativo que se ha redondeado a cero. En las propias especificaciones del estándar se afirma que este valor hace que sea mucho más sencillo conseguir una buena precisión numérica en determinados problemas críticos, sobre todo si se calculan mediante funciones complejas elementales.

Las representaciones que permiten un cero negativo pueden llegar a ser una fuente de errores en programas si los desarrolladores de software no se dan cuenta (u olvidan) que, si bien ambos ceros se comportan como iguales ante comparaciones numéricas, son diferentes patrones de bits y dan resultados diferentes en algunas operaciones, como por ejemplo la división.

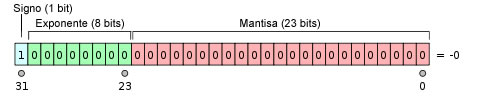
Representación binaria de 32 bits del cero negativo

Supongamos dos valores x e y, además de los dos ceros (positivo y negativo), los dos infinitos (positivo y negativo) y el anteriormente comentado valor NaN. En la siguiente tabla se muestran los distintos resultados que producirían las diferentes divisiones entre ellos (fila divido entre columna).

+z

-z

+∞

-∞

+0

-0

NaN

-z

+z

-∞

+∞

-0

+0

NaN

+0

-0

NaN

NaN

+0

-0

NaN

-0

+0

NaN

NaN

-0

+0

NaN

+∞

-∞

+∞

-∞

NaN

NaN

NaN

-∞

+∞

-∞

+∞

NaN

NaN

NaN

NaN

NaN

NaN

NaN

NaN

NaN

NaN

Vamos a ver un pequeño programa codificado en Java que demuestre algunos de los resultados anteriores. El tipo de datos float de Java tiene completamente integrado el estándar IEEE 754, por lo que no tendremos ningún problema para comprobar los cocientes.

Código

class CeroNegativo
{
 public static void main (String[] args)
 {
  float x,y,resultado;
  
  //+x:+y=+z
  x=1;
  y=1;
  resultado=x/y;
  System.out.println(x + "/" + y + "=" + resultado);
    
  //-x:-0=-infinito
  x=-1;
  y=0;
  resultado=x/y;
  System.out.println(x + "/" + y + "=" + resultado);
  
  //+x:-infinito=-0
  x=1;
  y=-1/new Float(-0.00);
  resultado=x/y;
  System.out.println(x + "/" + y + "=" + resultado);
  
  //0:0=NaN
  x=0;
  y=0;
  resultado=x/y;
  System.out.println(x + "/" + y + "=" + resultado);
 }
} 

Si nos fijamos en el segundo ejemplo (//+x:-infinito=-0), vemos que, como se explicaba en la tabla, un número positivo (+x) dividido entre menos infinito (−∞) da como resultado menos cero (-0). Para conseguir el valor de −∞, lo que hacemos es generar una división intermedia (-1/-0) cuyo cociente sea −∞ (siempre según la tabla), para que después este resultado pase a ser denominador del quebrado principal.

Esto anterior es perfectamente correcto en Java, y el resultado en línea de comandos sería lo siguiente.

Resultado

1.0/1.0=1.0
-1.0/0.0=-Infinity
1.0/-Infinity=-0.0
0.0/0.0=NaN

Otras operaciones aritméticas con -0 arrojan distintos resultados. La multiplicación, por ejemplo, sigue sus mismas reglas de combinación de signos, esto es -0 × -0 = +0, y la raíz cuadrada de -0 (√-0) es igual a -0. Veamos estos dos ejemplitos en código Java.

Código

import java.lang.Math;
 
class CeroNegativo
{
 public static void main (String[] args)
 {
  float x,y,resultado;
    
  //(-0)+(-0)=-0 
  x=new Float(-0.00);
  y=new Float(-0.00);
  resultado=x+y;
  System.out.println(x + "+" + y + "=" + resultado);
  
  //SQRT(-0)=-0 
  x=new Float(-0.00);
  resultado=(float)Math.sqrt(x);
  System.out.println("La raíz cuadrada de " + x + " es " + resultado);
 }
}

Y el resultado en línea de comandos sería el que sigue.

Resultado

-0.0+-0.0=-0.0
La raíz cuadrada de -0.0 es -0.0

Con respecto a las comparaciones, se pueden utilizar los operadores comparativos usuales de los diversos lenguajes de programación, aunque, para evitar algunos errores, muchos lenguajes traen comparadores propios para este fin. Es el caso del método equals de la clase Double de Java.

Y aparte de la fricada informática que supone, ¿para qué demonios nos puede servir este absurdo número? Pues bien, como comentábamos al principio, en algunos ámbitos se puede utilizar de manera más o menos formal para establecer valores muy determinados. Por ejemplo, la notación -0 puede ser usada para indicar que se redondeó a cero un número negativo muy cercano a él. Esto puede ser útil cuando un signo negativo es significativo, por ejemplo en la tabulación de temperaturas en grados Celsius, donde un signo negativo significa algo muy preciso (temperaturas bajo cero). En este caso querría decir que la temperatura es algo inferior a cero, pero por próxima se redondeó.

Otro caso práctico sería el de la física estadística, en la que, a veces, se usan temperaturas negativas para describir sistemas con una inversión de población, que se puede considerar que tienen una temperatura mayor que el infinito positivo. En este contexto, una temperatura de cero negativo es una temperatura (teórica) más grande que cualquier otra temperatura negativa, correspondiente al máximo concebible de inversión de población.

En fin, que prácticamente el cero negativo es como un puñetero cero a la izquierda, o sea que no se utiliza para nada. Pero la próxima vez que algún matemático te diga que el -0 no existe, imprímele este post y explícale cómo los informáticos, a veces, tenemos ases en la manga que otros no tienen. Ajo y agua; lo siento mucho.

12 comentarios a “El cero negativo (-0) sí existe, lo siento mucho”